逻辑回归

3/20/2025 110 阅读

一、理论知识

什么是逻辑回归？

逻辑回归（Logistic Regression）是一种常用的分类算法，尽管它的名字中有"回归"二字，但它实际上是用来解决分类问题的。可以把它想象成一个决策者，它会根据给定的特征来判断某个事件发生的概率。

逻辑回归的核心思想

想象你是一名医生，需要判断病人是否患有某种疾病。你会考虑多种因素：体温、血压、年龄等。逻辑回归就像是你的思考过程：

收集各种特征（体温、血压等）
给每个特征分配一个"重要性权重"
综合考虑所有因素，计算患病概率
如果概率超过某个阈值（比如50%），就判断为"患病"

逻辑回归的数学原理

逻辑回归的核心是Sigmoid函数：

$$S(z) = \frac{1}{1 + e^{-z}}$$

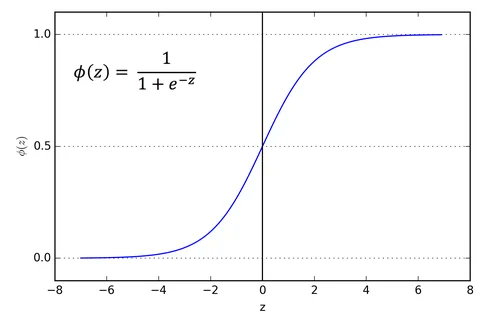
这个函数有个很好的特性：无论输入值z是多少，输出总是在0到1之间，可以解释为概率。

在逻辑回归中：

z是特征的线性组合：
$$z = w_1x_1 + w_2x_2 + … + w_nx_n + b$$
S(z)表示事件发生的概率
如果S(z) > 0.5，预测为正类（如患病）
如果S(z) < 0.5，预测为负类（如健康）

二、逻辑回归实例

实例：预测学生是否会通过考试

想象我们有一些学生的数据，包括他们的学习时间（小时）和是否通过考试的结果：

学习时间（小时）	是否通过考试
1	0（未通过）
2	0（未通过）
4	1（通过）
5	1（通过）
7	1（通过）

我们想建立一个模型，预测一个学习了3小时的学生是否会通过考试。

直观理解

从数据中我们可以看出一个趋势：学习时间越长，通过考试的可能性越大。逻辑回归会找到一个"临界点"，在这个点上，通过考试的概率为50%。

比如，模型可能会发现：

学习不到2.5小时的学生，通过概率低于50%
学习超过2.5小时的学生，通过概率高于50%

所以，对于学习了3小时的学生，模型可能会预测他有约65%的概率通过考试，因此判断为"通过"。

三、代码实现

下面我们用sklearn实现这个例子：

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 准备数据
# 学习时间（小时）
X = np.array([[1], [2], [4], [5], [7]])
# 是否通过考试（0表示未通过，1表示通过）
y = np.array([0, 0, 1, 1, 1])
# 创建逻辑回归模型
model = LogisticRegression()
# 训练模型
model.fit(X, y)
# 打印模型参数
print("模型系数:", model.coef_)
print("模型截距:", model.intercept_)
# 预测新数据
study_time = 3
prediction = model.predict([[study_time]])
probability = model.predict_proba([[study_time]])
print(f"学习{study_time}小时的学生，预测是否通过考试:", "通过" if prediction[0] == 1 else "不通过")
print(f"通过考试的概率: {probability[0][1]:.2f}")

四、代码解释

1. 数据准备

X = np.array([[1], [2], [4], [5], [7]])
y = np.array([0, 0, 1, 1, 1])

这里我们创建了两个数组：

X：学习时间（特征）
y：是否通过考试（标签），0表示未通过，1表示通过

2. 创建和训练模型

model = LogisticRegression()
model.fit(X, y)

这两行代码创建了一个逻辑回归模型并用我们的数据进行训练。训练过程会找到最佳的系数和截距，使模型能够最准确地预测结果。

3. 查看模型参数

print("模型系数:", model.coef_)
print("模型截距:", model.intercept_)

这里我们打印出模型学到的参数：

coef_：特征的系数（权重），表示学习时间对通过考试的影响程度
intercept_：截距，表示基础通过率

4. 预测新数据

study_time = 3
prediction = model.predict([[study_time]])
probability = model.predict_proba([[study_time]])

这段代码预测学习3小时的学生是否会通过考试：

predict方法返回类别预测（0或1）
predict_proba方法返回属于各个类别的概率

五、逻辑回归的优缺点

优点

简单易解释，计算效率高
不容易过拟合
直接输出概率值
可以通过正则化来处理多重共线性

缺点

只能解决线性可分的问题
对异常值敏感
特征之间需要相对独立
需要更多数据才能获得稳定的概率估计

六、小结

逻辑回归是一种简单而强大的分类算法，它通过Sigmoid函数将线性回归的结果转换为0到1之间的概率值，从而实现二分类。

在我们的例子中，逻辑回归成功地学习了学习时间与通过考试之间的关系，并能够预测新学生通过考试的概率。这种方法可以扩展到更多特征和更复杂的场景。

逻辑回归的核心优势在于其简单性和可解释性，使其成为许多分类任务的首选算法，特别是在需要理解特征重要性的场景中。

尽管它有一些局限性，如只能处理线性可分的问题，但在实际应用中，我们可以通过特征工程或结合其他算法来克服这些限制。

总之，逻辑回归是机器学习工具箱中的基础工具，掌握它对于理解更复杂的分类算法非常重要。

文章大纲