K-means聚类算法

3/18/2025 128 阅读

一、理论知识

什么是K-means聚类算法？

K-means是一种最常用的无监督学习算法，用于将数据分成K个不同的簇(cluster)。与KNN不同，K-means是一种无监督学习方法，不需要标签数据，它通过数据点之间的相似性（通常是距离）来进行分组。

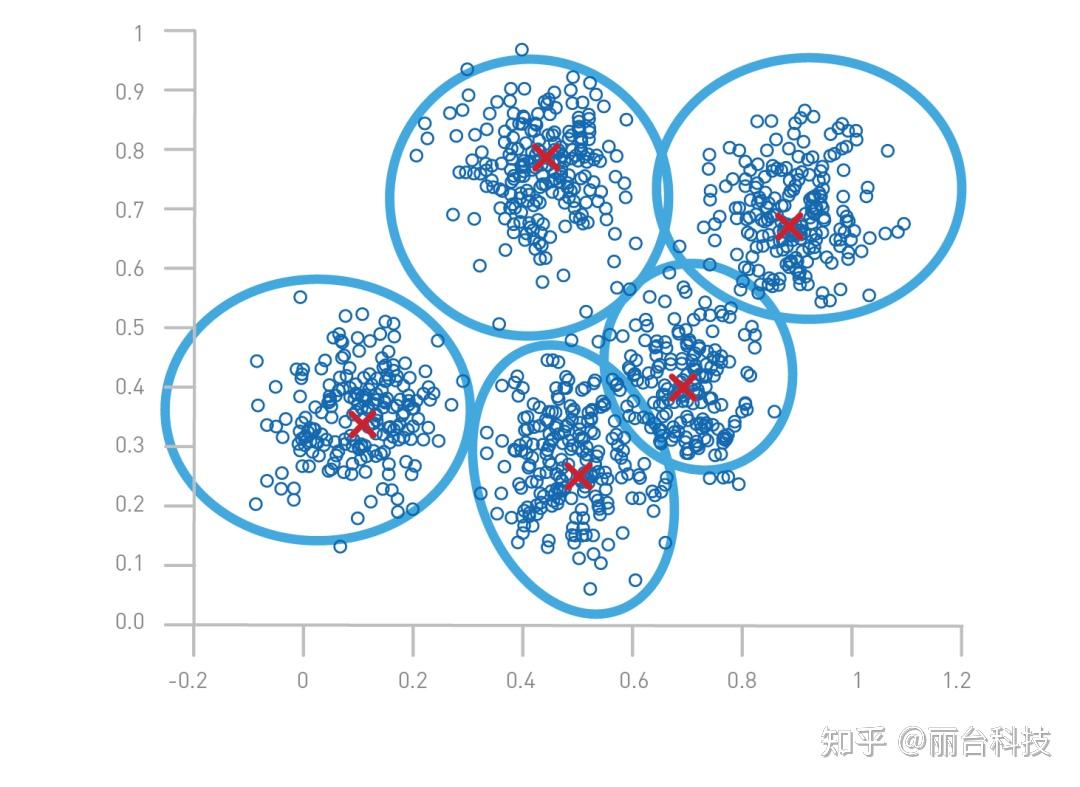
K-means的工作原理

K-means算法的基本步骤如下：

初始化：随机选择K个点作为初始聚类中心
分配：将每个数据点分配到最近的聚类中心所在的簇
更新：重新计算每个簇的中心点（取簇内所有点的平均值）
迭代：重复步骤2和3，直到聚类中心基本不再变化或达到最大迭代次数

距离计算方法

K-means通常使用欧氏距离来衡量数据点之间的相似性：

欧氏距离：
$\sqrt{(x_1-y_1)^2 + (x_2-y_2)^2 + … + (x_n-y_n)^2}$

K值的选择

选择合适的K值是K-means算法的关键：

K值太小：可能会将不同类别的数据归为一类
K值太大：可能会将同一类别的数据分成多类
常用方法：肘部法则(Elbow Method)、轮廓系数(Silhouette Coefficient)等

二、代码详解

下面我们来看一个简单的K-means聚类示例：

# 导入必要的库
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

# 创建示例数据
# 生成三组不同的数据点
np.random.seed(0)
# 第一组数据，围绕(0,0)
X1 = np.random.randn(100, 2) * 0.5
# 第二组数据，围绕(5,5)
X2 = np.random.randn(100, 2) * 0.5 + np.array([5, 5])
# 第三组数据，围绕(0,5)
X3 = np.random.randn(100, 2) * 0.5 + np.array([0, 5])
# 合并所有数据
X = np.vstack([X1, X2, X3])

# 实例化K-means模型
# n_clusters=3表示我们想要将数据分成3个簇
kmeans = KMeans(n_clusters=3, random_state=0)

# 训练模型
# fit方法会执行聚类过程
kmeans.fit(X)

# 获取聚类结果
labels = kmeans.labels_  # 每个数据点的簇标签
centers = kmeans.cluster_centers_  # 聚类中心点

# 预测新数据点的簇标签
new_points = np.array([[0, 0], [5, 5], [0, 5]])
new_labels = kmeans.predict(new_points)
print("新数据点的簇标签:", new_labels)

# 可视化聚类结果
plt.figure(figsize=(10, 6))
# 绘制原始数据点，颜色根据簇标签区分
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', alpha=0.7)
# 绘制聚类中心
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, alpha=0.9)
# 绘制新数据点
plt.scatter(new_points[:, 0], new_points[:, 1], c=new_labels, marker='*', s=200, edgecolors='black')

plt.title('K-means聚类结果 (K=3)')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.show()

三、代码解释

1. 导入必要的库

from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

这里我们导入了三个库：

KMeans：scikit-learn中的K-means聚类实现
numpy：用于数值计算和数组操作
matplotlib.pyplot：用于数据可视化

2. 创建示例数据

np.random.seed(0)
X1 = np.random.randn(100, 2) * 0.5
X2 = np.random.randn(100, 2) * 0.5 + np.array([5, 5])
X3 = np.random.randn(100, 2) * 0.5 + np.array([0, 5])
X = np.vstack([X1, X2, X3])

这段代码创建了三组数据点，每组100个点，分布在不同的区域：

第一组围绕(0,0)
第二组围绕(5,5)
第三组围绕(0,5)

然后将这三组数据垂直堆叠在一起，形成一个300×2的数组。

3. 实例化K-means模型

kmeans = KMeans(n_clusters=3, random_state=0)

这行代码创建了一个K-means模型，参数说明：

n_clusters=3：指定要将数据分成3个簇
random_state=0：设置随机种子，确保结果可重现

4. 训练模型

kmeans.fit(X)

fit方法执行K-means聚类过程：

随机初始化3个聚类中心
将每个数据点分配到最近的聚类中心
重新计算每个簇的中心点
重复步骤2和3，直到收敛

5. 获取聚类结果

labels = kmeans.labels_
centers = kmeans.cluster_centers_

聚类完成后，我们可以获取两个重要信息：

labels_：每个数据点所属的簇标签（0, 1或2）
cluster_centers_：3个聚类中心的坐标

6. 预测新数据点

new_points = np.array([[0, 0], [5, 5], [0, 5]])
new_labels = kmeans.predict(new_points)

这里我们创建了3个新的数据点，并使用训练好的模型预测它们分别属于哪个簇。predict方法会计算每个新点到各个聚类中心的距离，并将其分配到最近的簇。

7. 可视化聚类结果

plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', alpha=0.7)
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='X', s=200, alpha=0.9)
plt.scatter(new_points[:, 0], new_points[:, 1], c=new_labels, marker='*', s=200, edgecolors='black')

这段代码绘制了聚类结果：

原始数据点，颜色根据簇标签区分
聚类中心，用红色X标记
新数据点，用星号标记

四、K-means的优缺点

优点

简单易实现，计算效率高
对大数据集也能有效处理
当簇是凸形且大小相近时效果好

缺点

需要预先指定K值
对初始聚类中心敏感
只能发现球形簇，不适合发现复杂形状的簇
对异常值敏感

五、K-means的应用场景

K-means广泛应用于各种领域：

客户分群：根据消费行为将客户分成不同群体
图像分割：将图像分割成不同区域
文档聚类：根据内容相似性对文档进行分组
异常检测：识别与主要簇相距较远的点

六、小结

K-means是一种简单而强大的聚类算法，通过迭代优化将数据分成K个不同的簇。它的核心思想是最小化每个数据点到其所属簇中心的距离平方和。

虽然K-means有一些局限性，如需要预先指定K值、只能发现球形簇等，但由于其简单性和效率，它仍然是最常用的聚类算法之一。

在实际应用中，我们通常需要尝试不同的K值，并结合领域知识来选择最合适的聚类结果。

文章大纲